二次函数对称轴性质知识点总结（中考重要考点二次函数的图像与性质）

在初中的数学学习中，二次函数是非常重要的章节，而且里面涉及的考点非常的多，不管是在对应学期的各种考试，还是在中考时，都是比较热门的考点，而作为即将升入初三，面临着新的知识，同学们更应该将这部分内容理解掌握，也有利于最后的复习，今天我和同学们一起学习中考比较重要的一个基础考点，二次函数的图像与性质，这里不需要同学们死记硬背，而是学会运用观察法，比较法熟练的掌握，结合图像研究其性质及不同图像之间的相互关系，从简单的y=ax²(a≠0)开始通过分类详解，归纳总结，循序渐进的学习y=ax²+bx+c(a≠0),归纳出规律，从而彻底学会掌握。

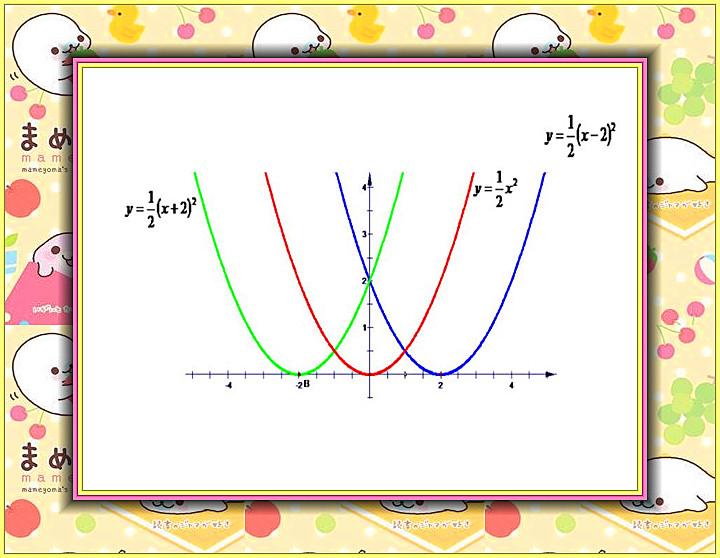
一、二次函数y=ax²(a≠0)的图像和性质

二次函数y=ax²(a≠0)图象的作法：①列表：在二次函数y=ax²(a≠0)中，自变量x的取值范围是全体实数，给出x的一些代表值，求出对应的y值，一般取5个或7个点，作为顶点的原点(0,0)是必取的，然后在y轴的两侧各取2个或3个点，注意对称取点；②描点：一般先描出对称轴一侧的几个点，再根据对称性找出另一侧的几个点；③连线：按照自变量由小到大的顺序，用平滑的曲线连接所描的点，两端无限延伸。注意：二次函数y=ax²(a≠0)的图象是一条抛物线，它的对称轴是y轴，顶点是原点（0,0)。

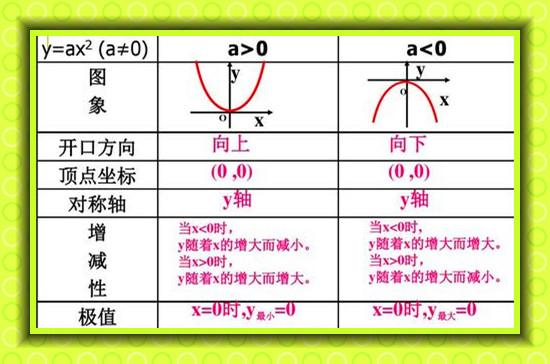
需要特别提醒的是，二次函数以对称轴为“界”，在对称轴的左右两侧，它的增减性是恰好相反的，而且在做题的时候，一定要注意说明其图像是在对称轴的左侧还是右侧，否则可能会出现错误。在做题的时候利用图像去分析是解决问题的最有效途径，数形结合思想也是本章重要的数学思想之一。

二、二次函数y=ax²+k(a≠0)的图像和性质

二次函数y=ax²+k(a≠0)的图像也是一条抛物线，它是由y=ax²向上或者向下平移|k|个单位得到的。

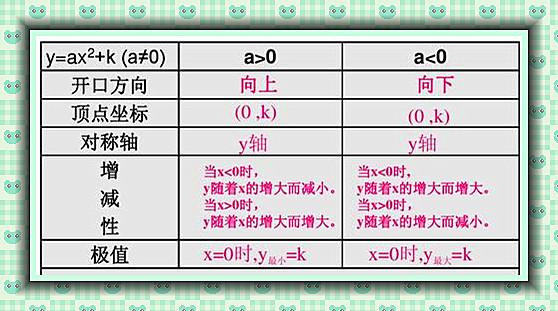
关于y=ax²+k(a≠0)的增减性其实和k的值是没有关系的，这里需要格外注意的是顶点坐标。

三、二次函数y=a(x+h)²(a≠0)的图像和性质

二次函数y=a(x+h)²(a≠0),它是由y=ax²向左或者向右平移|h|个单位得到的。

在学习二次函数y=a(x+h)²(a≠0)的图像与性质时，可类比二次函数y=ax²的图像与性质来学习。在a相等的情况下，两个函数图像的形状、开口方向等完全相同，只是位置发生了变化。顶点坐标由（0,0)变成了（-h,0),求抛物线y=a(x+h)²(a≠0)的对称轴时，只需x+h=0,即可得出x=-h。

四、二次函数y=a(x-h)²+k(a≠0)的图像和性质

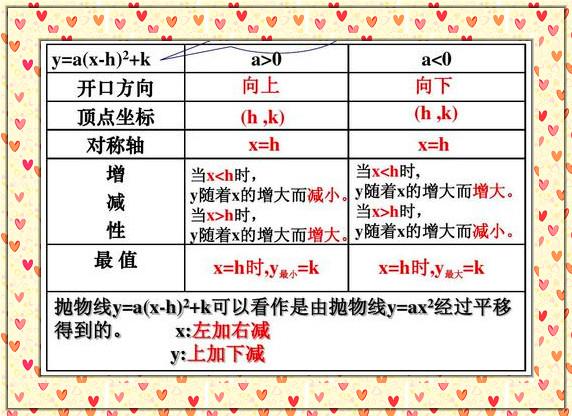
由于从y=a(x-h)²+k(a≠0)中可以直接看出抛物线的顶点坐标，因此通常也把y=a(x-h)²+k(a≠0)叫做二次函数的顶点式。

五、二次函数y=ax²+bx+c(a≠0)的图像和性质

二次函数y=ax²+bx+c(a≠0)的图象的画法：(1)描点法，步骤如下：①把y=ax²+bx+c(a≠0)化成y=a(x-h)²+k的形式；②确定抛物线的开口方向、对称轴和顶点坐标；③在对称轴两侧，以顶点为中心，左右对称描点画图。(2)平移法，步骤如下：①把y=ax²+bx+c(a≠0)化成y=a(x-h)²+k的形式，确定其顶点（h,k)；②作出函数y=ax²的图像；③将函数y=ax²的图像平移，使其顶点平移到（h,k)。

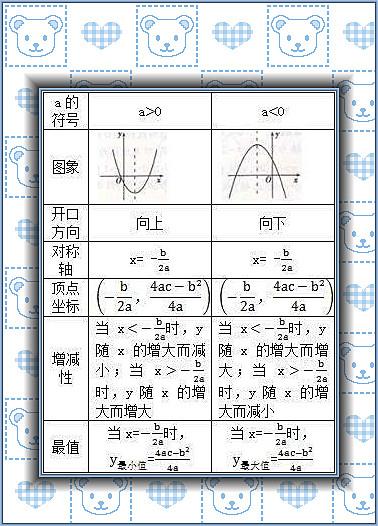
通过各种形式的二次函数图像，分类详解了他们的性质，希望同学们能够掌握，在以后的做题中，熟练运用。